Caching with Collatz

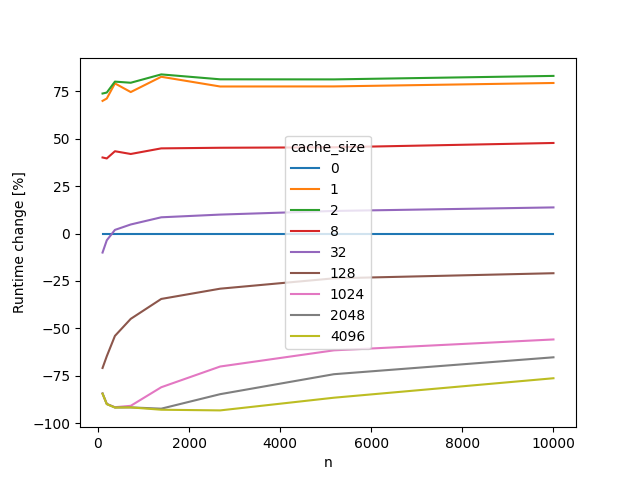
Recursion is a convenient way to express various math problems. The Fibonnacci sequence is the classic example. The Collatz conjecture is another. Computationally, recursion is often a poor choice for these problems (despite being convenient for mathematical analysis), so let’s see how we can speed it up by avoiding redundant calculations.

from functools import lru_cache
import time
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt


# have to benchmark carefully so that replicates don't use an existing cache.
# not sure how to do that w/ perfplot, so DIY:
reps = 10
sizes = np.logspace(2, 4, num=8).astype(int)
cache_sizes = [0, 1, 2, 8, 32, 128, 1024, 2048, 4096]
results = []

for n in sizes:
    for cache_size in cache_sizes:
        for _ in range(reps):

            def collatz(n):
                if n == 1:
                    return 0
                return 1 + collatz(n//2 if n % 2 == 0 else 3*n+1)

            if cache_size != 0:
                collatz = lru_cache(maxsize=cache_size)(collatz)

            st = time.time()
            _ = list(map(collatz, range(1, n)))
            ed = time.time()

            results.append({
                'n': n, 'cache_size': cache_size, 'elapsed': ed - st,
            })

df = pd.DataFrame(results)
pivot = df.pivot_table('elapsed', 'n', 'cache_size', aggfunc=np.median)
pivot.divide(pivot[0], axis=0).subtract(1).multiply(100).plot()
plt.ylabel('Runtime change [%]')
plt.show()

previous

LZ4 Compresion

next

Pandas efficiency