Note
Click here to download the full example code
Newton Fractals¶
Applying Newton’s method to a polynomial \(\mathbb{C} \rightarrow \mathbb{C}\) with multiple roots can converge to different roots depending on the starting point. The below plots color by root reached based on the starting point in the complex plane. These plots are examples of Newton Fractals.
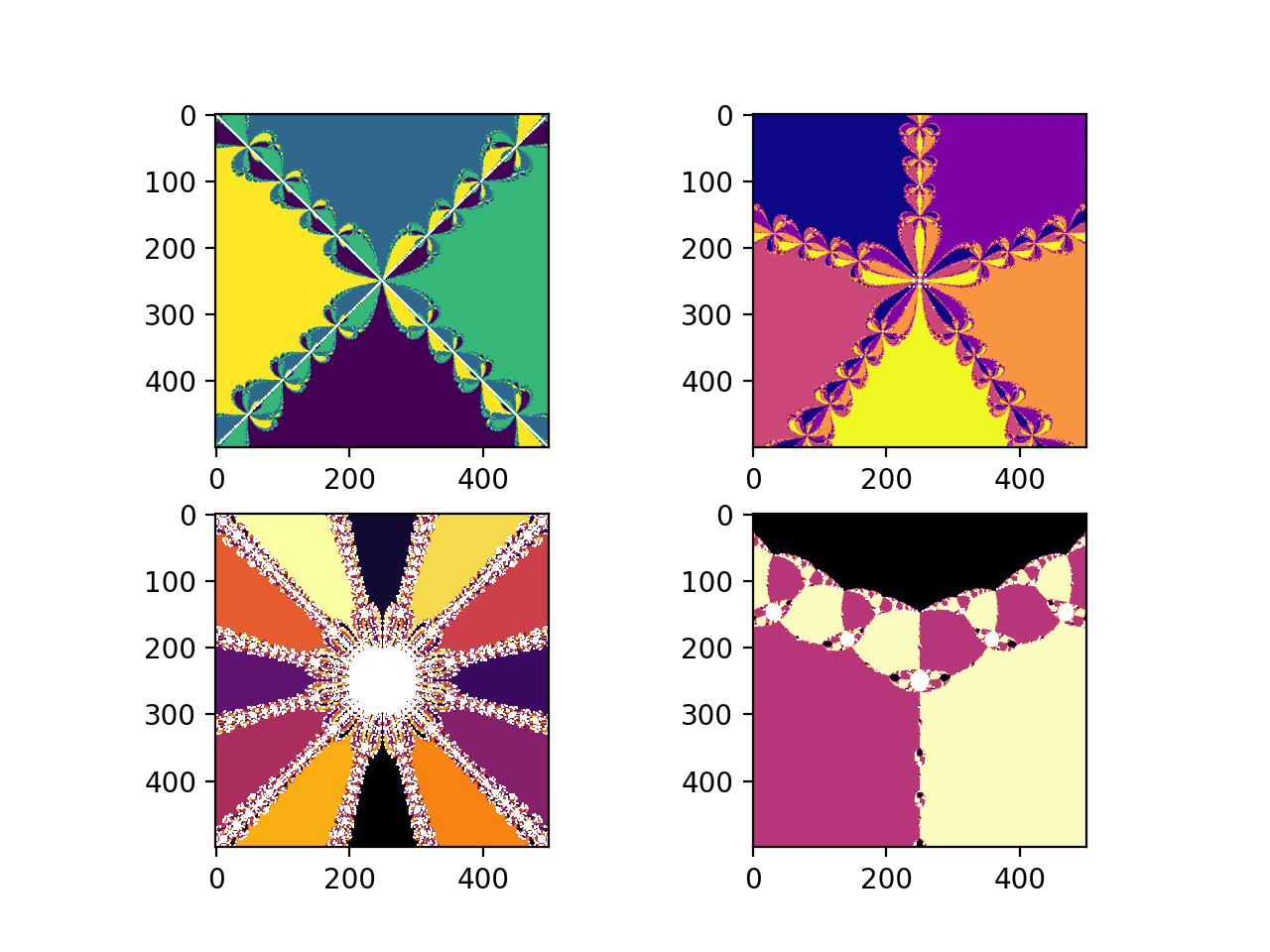
Out:
/home/kevin/projects/kevbase/sphinx/examples/misc/newton-fractals.py:22: RuntimeWarning: overflow encountered in power
(lambda z: z**12 - 1, lambda z: 12*z**11, [1, -1, 1j, -1j, (1+1j*3**0.5)/2, (1-1j*3**0.5)/2,
/home/kevin/projects/kevbase/sphinx/examples/misc/newton-fractals.py:22: RuntimeWarning: invalid value encountered in power
(lambda z: z**12 - 1, lambda z: 12*z**11, [1, -1, 1j, -1j, (1+1j*3**0.5)/2, (1-1j*3**0.5)/2,
/home/kevin/projects/kevbase/sphinx/examples/misc/newton-fractals.py:22: RuntimeWarning: invalid value encountered in multiply
(lambda z: z**12 - 1, lambda z: 12*z**11, [1, -1, 1j, -1j, (1+1j*3**0.5)/2, (1-1j*3**0.5)/2,
import numpy as np
import matplotlib.pyplot as plt
a = np.linspace(-2, 2, 500)
b = np.linspace(-2, 2, 500)
z = a[:, None] + b*1j
cases = [
(lambda z: (z**2 - 1)*(z**2 + 1), lambda z: 2*z *((z**2 - 1) + (z**2 + 1)), [1, -1, 1j, -1j]),
(lambda z: z**5 - 1, lambda z: 5*z**4, [-(-1)**(1/5), (-1)**0.8, -(-1)**0.6, (-1)**0.4, 1]),
(lambda z: z**12 - 1, lambda z: 12*z**11, [1, -1, 1j, -1j, (1+1j*3**0.5)/2, (1-1j*3**0.5)/2,
(-1+1j*3**0.5)/2, (-1-1j*3**0.5)/2, (3**0.5+1j)/2,
(3**0.5-1j)/2, (-3**0.5+1j)/2, (-3**0.5-1j)/2]),
(lambda z: z**3-2*z+2, lambda z: 3*z**2-2, [
-(9-57**0.5)**(1/3)/(3**(2/3)) - 2/(3*(9-57**0.5))**(1/3),
(1+3**0.5*1j)*(9-57**0.5)**(1/3)/(2*3**(2/3)) + (1-3**0.5*1j)/(3*(9-57**0.5))**(1/3),
(1-3**0.5*1j)*(9-57**0.5)**(1/3)/(2*3**(2/3)) + (1+3**0.5*1j)/(3*(9-57**0.5))**(1/3)]),
]
def naive_newton(f, fp, z0, n=100):
z = z0
for i in range(n):
z = z - f(z)/fp(z)
return z
def match_roots(approx, exact):
matches = np.empty_like(approx_roots, dtype=float) * np.nan
for i, true_root in enumerate(exact):
matches = np.where(np.abs(approx - true_root) < 1e-6, i, matches)
return matches
fig, axes = plt.subplots(2, 2, dpi=200)
axes = axes.ravel()
cmaps = ['viridis', 'plasma', 'inferno', 'magma']
for i, (f, fp, true_roots) in enumerate(cases):
approx_roots = naive_newton(f, fp, z)
exact_roots = match_roots(approx_roots, true_roots)
axes[i].imshow(exact_roots, cmap=cmaps[i])
Total running time of the script: ( 0 minutes 5.079 seconds)