Benford’s Law

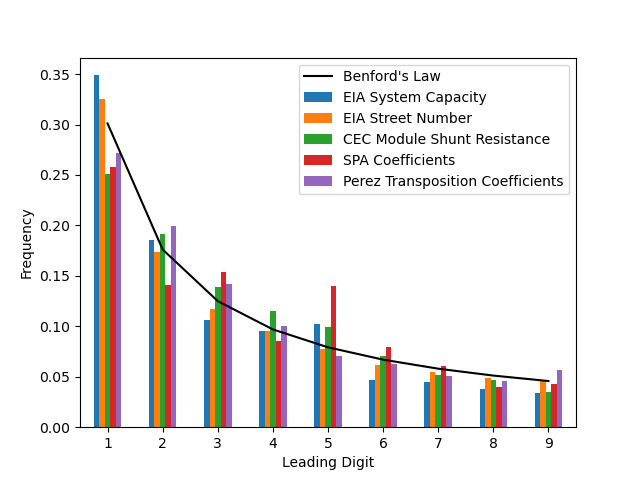
Many numerical datasets obey Benford’s Law 1, a phenomenon where the leading digit of numbers tend to be small. This has to do with the logarithmic spacing of values generated by power laws.

This snippet examines the distribution of leading digits in several PV-related collections of numbers and compares with the theoretical expectation. The datasets examined here are the EIA power plant database 2, the CEC PV module database 3, the coefficients used in the Solar Position Algorithm 4, and the coefficients used in the Perez transposition algorithm 5.

References

1

Benford’s Law: https://en.wikipedia.org/wiki/Benford%27s_law

2

https://www.eia.gov/electricity/data/browser/

3

https://github.com/NREL/SAM/blob/develop/deploy/libraries/CEC%20Modules.csv

4

https://www.nrel.gov/docs/fy08osti/34302.pdf

5

Perez, R., Ineichen, P., Seals, R., Michalsky, J., Stewart, R., 1990. Modeling daylight availability and irradiance components from direct and global irradiance. Solar Energy 44 (5), 271-289.

import pandas as pd
import numpy as np
import pvlib
import matplotlib.pyplot as plt

datasets = {}

filename = 'PowerPlants_US_202004.csv'
df = pd.read_csv(filename)
capacities = df.loc[df['Total_MW'] > 0, 'Total_MW']
street_numbers = pd.to_numeric(df['Street_Add'].str.split(" ").str[0], errors='coerce')
street_numbers = street_numbers[street_numbers != 0].dropna()
datasets['EIA System Capacity'] = capacities
datasets['EIA Street Number'] = street_numbers

df = pvlib.pvsystem.retrieve_sam('CECmod').T
r_sh = df['R_sh_ref'].dropna()
datasets['CEC Module Shunt Resistance'] = r_sh

spa_constants = np.hstack([
    np.hstack(list(map(np.ravel, pvlib.spa.TABLE_1_DICT.values()))),
    np.hstack(list(map(np.ravel, pvlib.spa.NUTATION_ABCD_ARRAY)))
])
spa_constants = spa_constants[spa_constants > 0]
datasets['SPA Coefficients'] = spa_constants

keys = ['allsitescomposite1990', 'allsitescomposite1988', 'sandiacomposite1988',
        'usacomposite1988', 'france1988', 'phoenix1988', 'elmonte1988', 'osage1988',
        'albuquerque1988', 'capecanaveral1988', 'albany1988']
perez_constants = np.hstack([
    np.ravel(pvlib.irradiance._get_perez_coefficients(key)) for key in keys
])
perez_constants = abs(perez_constants[perez_constants != 0])
datasets['Perez Transposition Coefficients'] = perez_constants

def get_leading_digit_distribution(data):
    first_digits = [int("{:e}".format(x)[0]) for x in data]
    digit_counts = pd.Series(first_digits).groupby(first_digits).count()
    N = digit_counts.sum()
    digit_fractions = digit_counts / N
    return digit_fractions


digit_fractions = pd.DataFrame({
    name: get_leading_digit_distribution(data)
    for name, data in datasets.items()
})

d = np.arange(1, 10)
expected_fractions = np.log10(1 + 1/d)

digit_fractions.plot.bar(rot=0)
plt.plot(expected_fractions, c='k', label="Benford's Law")
plt.legend()
plt.ylabel('Frequency')
plt.xlabel('Leading Digit')

Out:

Text(0.5, 23.52222222222222, 'Leading Digit')

previous

Reflections

next

PyPI Package Versions